trying to ascend
Oldcel KHHV
★★★★★
- Joined
- Aug 30, 2020
- Posts
- 15,931
How many anagrams, whose consonants are not together, can be formed with the word EFICIALATE
Wrong86,400
5!*6P5
No604800?
We distinguish four cases:How many anagrams, whose consonants are not together, can be formed with the word EFICIALATE
CorrectWe distinguish four cases:
All in all, there are therefore 4!*6!/(2*2*2)*((5 choose 1)+3*(5 choose 2)) = 3*6!*(5+3*10) = 3*6!*35 = 15*7! = 15*5040 = 75600 anagrams without consecutive consonants
- Neither the first nor the last letter is a consonant. Using stars and bars we find that there are 4!*6!/(2*2*2)*(6-1 choose 4) such anagrams (the 4! accounts for all the possible ways to order the 4 consonants and the 6!/(2*2*2) accounts for all the possible ways to order the 6 vowels (where we need to divide by 2 thrice because all three distinct vowels appear twice))
- Only the first letter is a consonant. Using stars and bars again we find that there are 4!*6!/(2*2*2)*(6-1 choose 3) such anagrams
- Only the last letter is a consonant. By symmetry there are 4!*6!/(2*2*2)*(6-1 choose 3) such anagrams as well
- Both the first and the last letter are consonants. Using stars and bars one last time we find that there are 4!*6!/(2*2*2)*(6-1 choose 2) such anagrams
Giga mogger iqWe distinguish four cases:
All in all, there are therefore 4!*6!/(2*2*2)*((5 choose 1)+3*(5 choose 2)) = 3*6!*(5+3*10) = 3*6!*35 = 15*7! = 15*5040 = 75600 anagrams without consecutive consonants
- Neither the first nor the last letter is a consonant. Using stars and bars we find that there are 4!*6!/(2*2*2)*(6-1 choose 4) such anagrams (the 4! accounts for all the possible ways to order the 4 consonants and the 6!/(2*2*2) accounts for all the possible ways to order the 6 vowels (where we need to divide by 2 thrice because all three distinct vowels appear twice))
- Only the first letter is a consonant. Using stars and bars again we find that there are 4!*6!/(2*2*2)*(6-1 choose 3) such anagrams
- Only the last letter is a consonant. By symmetry there are 4!*6!/(2*2*2)*(6-1 choose 3) such anagrams as well
- Both the first and the last letter are consonants. Using stars and bars one last time we find that there are 4!*6!/(2*2*2)*(6-1 choose 2) such anagrams
For x < 1, y = -ln x, so its derivative is -1/x. For x > 1, y = ln x, so its derivative is 1/x. For x = 1, the derivative does not exist.y=|lnx|
Find the first order derivative of the above function
For x < 1, y = -ln x, so its derivative is -1/x. For x > 1, y = ln x, so its derivative is 1/x. For x = 1, the derivative does not exist.
Find all functions R (greater than 0)---->R (greater than 0), such that:For x < 1, y = -ln x, so its derivative is -1/x. For x > 1, y = ln x, so its derivative is 1/x. For x = 1, the derivative does not exist.
@trying to ascend help bro
Ah okayAs he pointed out, modulus is just the sqrt raised to the power of two (or the root of any even number raised to its inverse),
So you just have to apply the chain rule and you will find the value, though you have to restrict the domain for it to work
@trying to ascend help bro
Yeah but I've been using him and another YouTube channel called blackpenredpen to revise for my final math examhis answer is the same as mine, just way more complicated
ah ok good luckYeah but I've been using him and another YouTube channel called blackpenredpen to revise for my final math exam
Thanks, it's all or nothing man, I've been failing like a bitchah ok good luck
You got a hint? I think I know the answer, but I ain't seeing how to prove it.Find all functions R (greater than 0)---->R (greater than 0), such that:
f(xy + f(x)) = f(f(x)f(y)) + x
This, along with the incenter and pi plane problems, was one of the only problems I couldn't solve by myself, so I can't give much details.You got a hint? I think I know the answer, but I ain't seeing how to prove it.
This, along with the incenter and pi plane problems, was one of the only problems I couldn't solve by myself, so I can't give much details.
Either way, the solution is here (though it's not in english):
View: https://www.youtube.com/watch?v=OoCSBMZkZLY
Let u = lg x. Then F(x) = u^4 + 12u^2(3 - u) = u^2(u^2 - 12u + 36) = u^2(u - 6)^2 = (u(6 - u))^2, which is clearly maximal when u = 3, in which case the function takes the value 9^2 = 81.All logs are in base 2.
Knowing that x belongs to the closed interval (1, 64), find the maximum value of the follwing function
F(x) = (logx) to the power of 4 + 12(logx) to the power of 2 . log(8/x)
CorrectLet u = lg x. Then F(x) = u^4 + 12u^2(3 - u) = u^2(u^2 - 12u + 36) = u^2(u - 6)^2 = (u(6 - u))^2, which is clearly maximal when u = 3, in which case the function takes the value 9^2 = 81.
seems good to meI need someone to check my answer
Find y prime:
x^y=y^x
Ans: y prime = [ln(y)-y/x]/[ln(x)-x/y]
using Markov chain methods I arrive at 32/79Three players sit in a desk to play a game.
Alternately, each player rolls a non vicious cubic dice and, after each player rolls it, the player to its right gets to play.
If 1 is rolled, then the player to its left gets to play.
The one who rolls 6 wins the game.
Given that, what are the odds of the player that played first to win the game (not necessarily in his first play)?
Correctusing Markov chain methods I arrive at 32/79
Circumference C has equation x² + y² = 16. Let C' be a circle of radius 1 that moves internally tangent to circle C, without slipping between the contact points, that is, C' rolls internally on C.
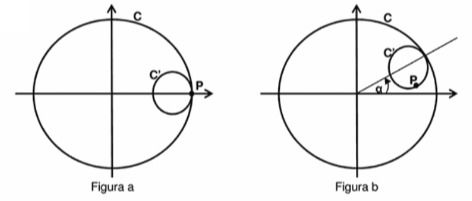
Point P on C' is defined so that at the beginning of the movement of C', point P coincides with the point of tangency (4,0), as shown in figure a. After a certain displacement, the angle between the x axis and the straight line joining the center of the circles is α, as shown in figure b.
Determine the coordinates of the point P marked on C' as a function of the angle α.
Here is a physics problem:I think I'll return to studying for my physics paper
Here is a physics problem:
Consider a capacitor octahedron, such that there is a capacitor between each vertex of capacitance C.
Each pair of vertex, sharing an edge or not, has a capacitor between it.
Calculate the equivalent capacitance between two neighbor vertex of the solid
x = 3cos(α) + cos(-3α) = 3cos(α) + cos(3α) & y = 3sin(α) + sin(-3α) = 3sin(α) - sin(3α)Circumference C has equation x² + y² = 16. Let C' be a circle of radius 1 that moves internally tangent to circle C, without slipping between the contact points, that is, C' rolls internally on C.

Point P on C' is defined so that at the beginning of the movement of C', point P coincides with the point of tangency (4,0), as shown in figure a. After a certain displacement, the angle between the x axis and the straight line joining the center of the circles is α, as shown in figure b.
Determine the coordinates of the point P marked on C' as a function of the angle α.
Correctx = 3cos(α) + cos(-3α) = 3cos(α) + cos(3α) & y = 3sin(α) + sin(-3α) = 3sin(α) - sin(3α)
Turkey is europe, inform yourselfYOU WON'T FIND ANY OOGAA KARABOGAS HERE!!!!!!!!!!!!! FUCKING NIGGERS
Sure, though I'm studying more physics nowadays, that's why the thread is often empty of new problems.@trying to ascend
hit me up with a math problem. i have an exam in a few minutes, but gimme something fun to come back to. i'll probably seriously keep up with this math problem thread just like the old one i used to do with @Divergent_Integral
Pass a hard entrance exam, become a STEM graduate in a good Uni, make >150k working at a big tech companyWhy would i care about this nerd shit
Why would i care about this nerd shit
L + ratio = pwnedPass a hard entrance exam, become a STEM graduate in a good Uni, make >150k working at a big tech company
@AhnfeltiaPass a hard entrance exam, become a STEM graduate in a good Uni, make >150k working at a big tech company
You don't say. Your post was pretty apt tho. I just wanted to make a shitty vaguely-math-related quip.@Ahnfeltia
oh whoops for some reason i thought this was the "Fun facts about incels" thread
I thought you were joking but after a quick search Duolingo does actually have a math-oriented whatchamacallit.I might learn math from Duolingo
you have a masters in math. you should be able to solve it. i could definitely solve it, i just need to read a wikipedia article on ellipses so i can understand wtf the terminology meansI should be right at home here with a masters in math but I don't know how to solve the penultimate problem, and I was always weak in geometry. I'm really good at calculus, though. Taking a derivative or inverse just seems to make it worse.





