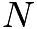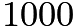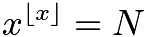trying to ascend
Oldcel KHHV
★★★★★
- Joined
- Aug 30, 2020
- Posts
- 15,931
Post all math related problems and solutions here. Don't cheat.
First problem: If the coefficients of x³ and x^4 in the expansion of (1+ ax+ bx² ) (1−2x) ^18 in powers of x are both zero, then (a, b) is equal to?
First problem: If the coefficients of x³ and x^4 in the expansion of (1+ ax+ bx² ) (1−2x) ^18 in powers of x are both zero, then (a, b) is equal to?