Shaktiman
Legend
★★★
- Joined
- May 24, 2022
- Posts
- 3,788
How the father’s height influences the son’s height
Let’s say the average height of men is 67.7 inches (172cm). If a man is 72 inches (183cm) tall, how tall will his full-grown son be?
How the father's height influences the son's height
Let’s say the average height of men is 67.7 inches (172cm). If a man is 72 inches (183cm) tall, how tall will his full-grown son be?
Your first instinct might be: "Oh, that's easy. The son will be as tall as his father."
Although 72 inches (183cm) is a possible guesstimate for the son's height, it is not very probable from a statistical point of view.
Correlation, regression, and standard deviation
Instead, we should compile datasets of the average height of sons whose fathers were 72 inches (183cm) tall.We will then repeat the step above for fathers of heights 58 inches (147cm), 59 inches (150cm), 60 inches (152cm), 61 inches (155cm), and so on, until 78 inches (198cm).
Next, we can draw a graph of averages between the heights of fathers (x-axis) and the heights of sons (y-axis). The plotted points 'x' mark the average height of sons whose fathers are of a particular height.
The regression line is a line of best fit with equation y=a+bx. Since the regression line is a straight line with a gradient b, the slope b will be the regression coefficient. The correlation coefficient is 0.5.
Now we can see that the father's height and the son's height are positively correlated, but only by a correlation coefficient of 0.5. Note that the slope of standard deviation (SD) line is less steep than the slope of the regression line. For every 1 SD increase in the father's height, the son's height increases by merely 0.5 SD.
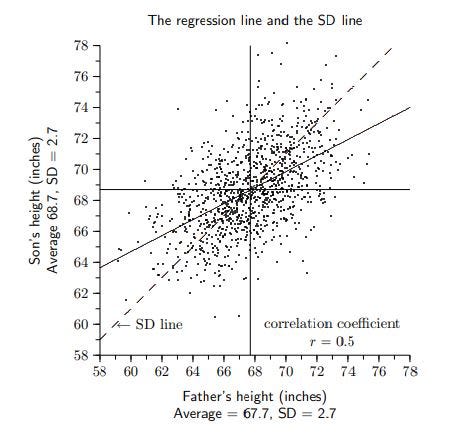
If you are a man with average height, you can expect your son to be a few inches (centimeters) taller than you.
This is because the regression line and the SD line both coincide at the average heights. For instance, a father with an average height of 67.7 inches (172cm) will have a 68.7-inch-tall (175cm-tall) son.
However, if you are much taller or shorter than average, the prediction will be obviously trickier.
A 78-inch-tall (198cm-tall) man will have a 74-inch-tall (188cm-tall) son. For an exceptionally tall man, his son will be around 4 inches (10cm) shorter than him. His son will still be taller than average.
A 58-inch-tall (147cm-tall) man will have a 63.5-inch-tall (161cm-tall) son. For an exceptionally short man, his son will be around 5.5 inches (14cm) taller than him. His son will still be shorter than average.
For fathers who are exceptionally tall or short, their sons will be taller or shorter than average, but by not so much as their fathers.
Back to our question
For someone with a 72-inch-tall (183cm-tall) father, we should predict the adult son's height by compromising on the regression correlation of father-son heights and the mean height of sons with 72-inch-tall (183cm-tall) fathers within the demogaphic. Our best guess for the adult son's height should regress towards the mean.Based on actual data from the heights of 1,078 fathers and sons in England, for fathers 72 inches (183cm) tall, their sons are 71 inches (180cm) tall on average.
Pearson's Father-Son Data (via University of Chicago)
Why the father's height is only part of the equation
Researchers at University of Chicago sought to explain this phenomenon.First, our heights are genetically influenced by the heights of both our parents. The study above did not explicitly consider the mothers' heights.
Statistically there are a lot more females with average height than exceptionally tall females with a few SDs taller than the average. Thus there is a fairly high chance that an exceptionally tall man might marry a woman who is not exceptionally tall, so their son will not be as exceptionally tall as the father.
Secondly, our heights are not solely determined by genetical or hereditary factors. It is also affected by environmental factors such as nutrition and exercise.
In 1884, a polymath statistician, Francis Galton, recruited 10,000 people to measure the heights of parents and children. He paid 3 pence to each participant. He found that the children's height deviation from the population mean was around two-thirds of the deviation of their parents.
In Galton's words, when parents are taller than mean, their children tend to be shorter than them. When parents are shorter than mean, their children tend to be taller than them.





