What's new

Welcome to Incels.is - Involuntary Celibate Forum

Welcome! This is a forum for involuntary celibates: people who lack a significant other. Are you lonely and wish you had someone in your life? You're not alone! Join our forum and talk to people just like you.
Log in Register

Follow Us On Social Media

Serious Daily math problem thread

prob #0010 can be solved by Mathematica, ngl :

$ wolframscript
Wolfram Language 12.1.1 Engine for Linux x86 (64-bit)
Copyright 1988-2020 Wolfram Research, Inc.

In[1]:= Solve[(A^3+B^3)/(A^3+C^3) == (A+B)/(A+C)]

Out[1]= {{B -> -A}, {C -> A - B}, {C -> B}}
 
WorldYamataizer said:
Problem #0010

While Lino was simplifying the fraction (A^3+B^3)/(A^3+C^3) he cancelled the threes (A^3+B^3)/(A^3+C^3)
to obtain the fraction (A+B)/(A+C). If B ≠ C, determine a necessary and sufficient condition on A,B and C for Lino's
method to actually yield the correct answer, i.e.. for (A^3+B^3)/(A^3+C^3)=(A+B)/(A+C).

@Divergent_Integral @SelfCrucified @grondilu @mNFwTJ3wz9 @Diocel @mental_out @Irredeemable @Caesercel @nihility @Liszt
Click to expand...
(A^3+B^3)/(A^3+C^3)=(A+B)/(A+C)
case 1 : numerator = 0 or Denominator = 0 or both
A = -B or A = -C or both

Otherwise :
(A^3+B^3) * (A + C) = (A^3+C^3) * (A + B)
A^4 + A^3 * C + B^3*A + B^3*C = A^4 + A^3 * B + C^3*A + C^3*B
A^3 * (C-B) + A * (B^3 - C^3)+ B^3*C = B*C( C^2 - B^2)

A^3 * (C-B) + A * (B^3 - C^3)+ B^3*C = B*C( C^2 - B^2)

dividing by B-C everywhere and B=C is a solution

-A^3 + A * (B^2 + BC + C^2) + B*C(B+C) = 0
A*(B^2 + C^2 - A^2) + B*C*(A + B + C) = 0
Now Apply Quadratic formula on B or C to get some really fucked Values I guess
grondilu said:
Wolfram Language 12.1.1 Engine for Linux x86 (64-bit)
Copyright 1988-2020 Wolfram Research, Inc.

In[1]:= Solve[(A^3+B^3)/(A^3+C^3) == (A+B)/(A+C)]

Out[1]= {{B -> -A}, {C -> A - B}, {C -> B}}
Click to expand...
Probably will get these
OK yeah it does simplify to :
-(A + B)*(A + C)*(A - B - C) = 0
 
Last edited:
Useful Fact for Problem #0010

a^3+b^3=(a+b)*(a^2-ab+b^2) for all real numbers a and b.

mNFwTJ3wz9 said:
Probably will get these
OK yeah it does simplify to :
-(A + B)*(A + C)*(A - B - C) = 0
Click to expand...
Nice algebraic persistence.
EDIT: Your brute force methods never fail to impress me
 
WorldYamataizer said:
EDIT: Your brute force methods never fail to impress me
Click to expand...
Thanks man.

I think brute force is really nice because even the proof for Riemann hypothesis can be brute forced in finite time (Even if it is BB(700 something))

Sadly I don't have enough persistence to continue with 9(c) The equations after rotation are just too bad, and the way of forcing integer values on the resultant equations are not obvious.
 
mNFwTJ3wz9 said:
Sadly I don't have enough persistence to continue with 9(c) The equations after rotation are just too bad, and the way of forcing integer values on the resultant equations are not obvious.
Click to expand...
Incel trait : Too busy having sex to bruteforce math equations.

WorldYamataizer said:
@Diocel @mental_out @Irredeemable @Caesercel @nihility @Liszt
Click to expand...
Truecel trait : Can't even take a 2 min break from seducing jb's to look at the math problems.

@Divergent_Integral @WorldYamataizer
Chad trait : Can't have sex, so cope with making math problems to solve with incels.
 
Solutions to Problem #0009

a. See the solution by @WorldYamataizer, post #144.

b. Using the result of Problem #0006(b), we only need to find a binary operation that expresses "minus" and "reciprocal", because we can express the four basic arithmetic operations in terms of those. In a sense both minus and reciprocal are self-inverse (conveniently disregarding the fact that reciprocal is unary and minus is binary). It seems reasonable then to combine them into one operation. One of the simplest such combinations is 1 / (x - y). And indeed x * y = 1 / (x - y) is immediately seen to work, since x * 0 = 1 / x and (x * y) * 0 = x - y.

c. Let A and B be two points in the set S. Then, with d denoting Euclidean distance, for all points C that belong S, we have d(A,C) - d(B,C) = an integer <= d(A,B), because of the triangle inequality and the assumption that all mutual distances be integers. Using the definition of a hyperbola as a locus of points such that the difference of distances from two foci is a constant, we thus see that C must lie on one element of a finite set of hyperbolas with one of their axes along line AB.

We will now argue by reductio ad absurdum. Suppose there is a point D of S that does not lie on the line AB. Then, by similar reasoning as before, all points C of S must lie on a finite set of hyperbolas with one of their axes along line BD. Thus we see that all points C of S must lie on the intersections of finitely many distinct hyperbolas. But that would make S a finite set, contrary to assumption.
 
Divergent_Integral said:
c. Let A and B be two points in the set S. Then, with d denoting Euclidean distance, for all points C that belong S, we have d(A,C) - d(B,C) = an integer <= d(A,B), because of the triangle inequality and the assumption that all mutual distances be integers. Using the definition of a hyperbola as a locus of points such that the difference of distances from two foci is a constant, we thus see that C must lie on one element of a finite set of hyperbolas with one of their axes along line AB.

We will now argue by reductio ad absurdum. Suppose there is a point D of S that does not lie on the line AB. Then, by similar reasoning as before, all points C of S must lie on a finite set of hyperbolas with one of their axes along line BD. Thus we see that all points C of S must lie on the intersections of finitely many distinct hyperbolas. But that would make S a finite set, contrary to assumption.
Click to expand...
Ok I'm going to need some time to process that
 
Do some statistics problems
 
Solutions to Problem #0010
Screenshot 13
Screenshot 15


Additionally, see post #156 by @mNFwTJ3wz9 for his solution.
 
a = 0.2
b = 0.3
c = 0.5
 
Problem #0011

Welcome to .co Math Club! Here's a problem to work on for today.

A diameter AB of a circle intersects a chord CD at the point E. If CE=7, DE=1 and ∠BED=pi/4 (45 degrees), then determine the radius of the circle.

@Divergent_Integral
@SelfCrucified
@grondilu
@mNFwTJ3wz9
@Diocel
@mental_out
@Irredeemable
@Caesercel
@nihility
@Liszt
 
WorldYamataizer said:
A diameter AB of a circle intersects a chord CD at the point E. If CE=7, DE=1 and ∠BED=pi/4 (45 degrees), then determine the radius of the circle.
Click to expand...
1609871853999

isnt there some theorem about the multiplication of the sections of the chords being some fixed value?
 
Fuck it, let's do it the old way
WorldYamataizer said:
Yes, that diagram works. What program do u use to make these pics? I use desmos tbh
Click to expand...
MS paint lmao
1609872094963

eqn 1
x1^2 + y1^2 = x2^2 + y2^2 = (x3 + y3)^2
now let's do the areas of triangles
 
Last edited:
WorldYamataizer said:
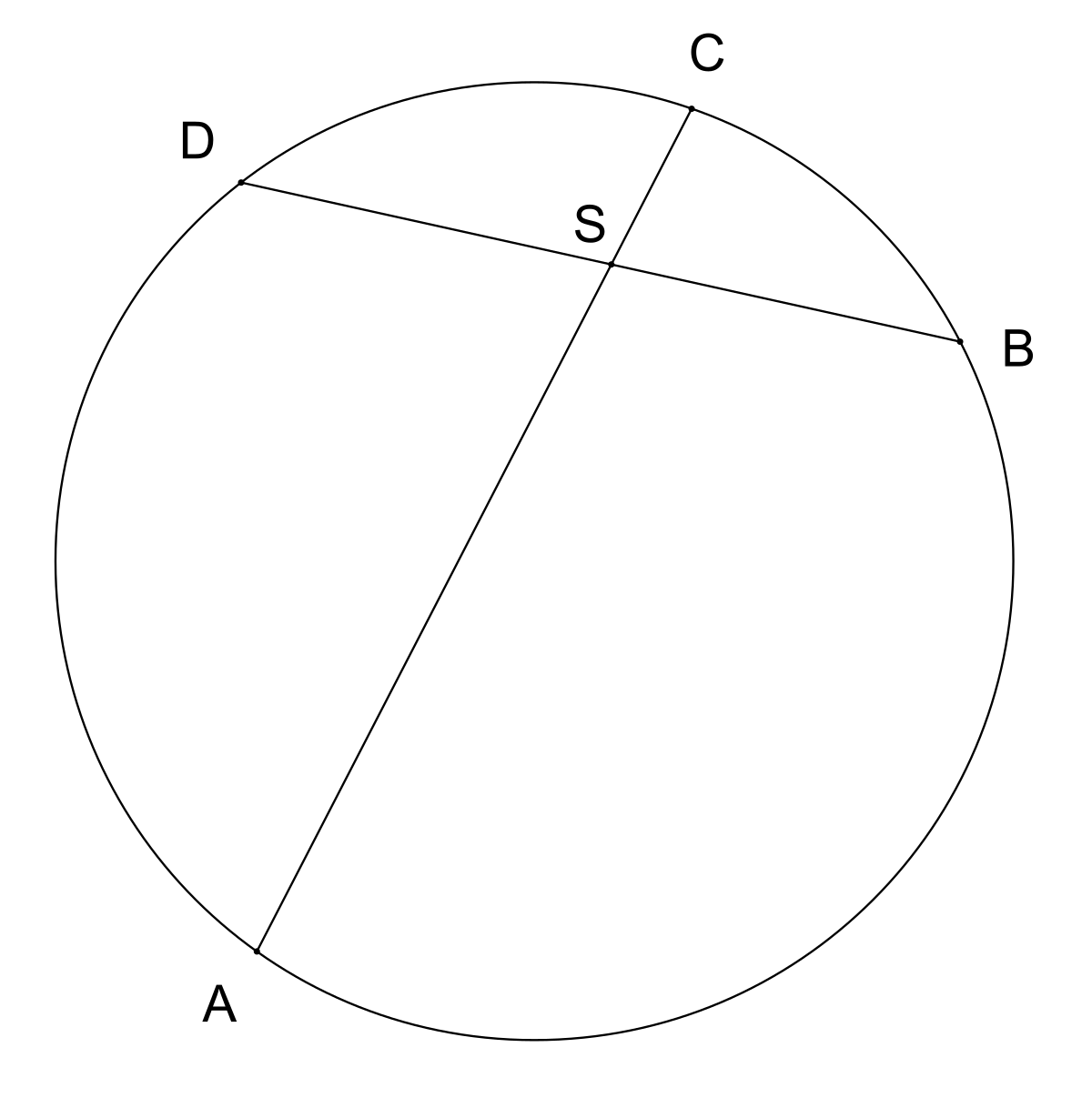
Yes
Maybe this wikipedia article has the one youre thinking of

en.m.wikipedia.org

Intersecting chords theorem - Wikipedia

en.m.wikipedia.org en.m.wikipedia.org
Click to expand...
I'll look it up after tbh
Let's just try to brute force for now, since it seems peaceful enough
1/2 * sin(135) * y3 * 7 + 1/2 * sin(45) * x3 * 7 = x1* y1 * 1/2
1/2 * sin(45) * y3 * 1 + 1/2 * sin(135) * x3 * 1 = x2* y2 * 1/2
lets simplify these 2 for now
since sin 135 and sin 45 are 1/sqrt(2)
x1*y1*sqrt(2) = 7y3 + 7x3
x2*y2*sqrt(2) = y3 + x3
lol I think this just derived the chord theorem
x1*y1 = 7*x2*y2
1609873291767

adding some Pythagoras stuff with the "height"
x1^2 = (x3 - 7/sqrt2)^2 + ( 7/sqrt2)^2
y1^2 = (y3 + 7/sqrt2)^2 + ( 7/sqrt2)^2


x2^2 = (x3 + 1/sqrt2)^2 + ( 1/sqrt2)^2
y2^2 = (y3 - 1/sqrt2)^2 + ( 1/sqrt2)^2
So the complete list of equations so far is :

x1^2 + y1^2 = x2^2 + y2^2 = (x3 + y3)^2
x1*y1 = 7*x2*y2 = (y3 + x3) * 7/sqrt2
x1^2 = (x3 - 7/sqrt2)^2 + ( 7/sqrt2)^2
y1^2 = (y3 + 7/sqrt2)^2 + ( 7/sqrt2)^2
x2^2 = (x3 + 1/sqrt2)^2 + ( 1/sqrt2)^2
y2^2 = (y3 - 1/sqrt2)^2 + ( 1/sqrt2)^2

which looks like it should be enough...
Lets start with
x1^2 + y1^2 = (x3 + y3)^2
(x3 - 7/sqrt2)^2 + ( 7/sqrt2)^2 + (y3 + 7/sqrt2)^2 + ( 7/sqrt2)^2 = (x3 + y3)^2
- 7 * sqrt2 * x3 + 49/2 + 49/2 + 7 * sqrt2 * y3 + 49/2 + 49/2 = 2 * x3 * y3
An nice, I think this somewhat solves things
 
Last edited:
Prob 0011. We can take E as an origin and fix C and D in a reference frame where AB will be on the horizontal axis (so we can use the 45° constraint). Let's note r2 the square root of 2.

C : (-r2/2*7, -r2/2*7)
E : (0, 0)
D : (r2/2, r2/2)

We just need to search the center of the circle, and it's the intersection of the horizontal axis with the bisector of CD. That should not be hard to put in equations. The diagram below is exact. I used Kig.

Capture dcran de 2021 01 05 20 27 15

Let's name I = (w, z) the middle of CD.
A point M(x,y) is on that bisector if and only if (x-w) + (y-z) = 0. We want the point for which y = 0, so x = w + z

Thus x = -3r2/2 + -3r2/2 = -3r2

So the radius is sqrt( (-3r2-r2/2)² + (r2/2)² ) = sqrt( (7r2/2)² + 1/2 ) = sqrt( 49/2 + 1/2 ) = sqrt(50/2) = sqrt(25) = 5

The fact that I get an integer gives me confidence I didn't make a mistake, but that's no guarantee ofc.
 
Last edited:
mNFwTJ3wz9 said:
which looks like it should be enough...
Lets start with
x1^2 + y1^2 = (x3 + y3)^2
(x3 - 7/sqrt2)^2 + ( 7/sqrt2)^2 + (y3 + 7/sqrt2)^2 + ( 7/sqrt2)^2 = (x3 + y3)^2
- 7 * sqrt2 * x3 + 49/2 + 49/2 + 7 * sqrt2 * y3 + 49/2 + 49/2 = 2 * x3 * y3
An nice, I think this somewhat solves things
Click to expand...
x2^2 + y2^2 = (x3 + y3)^2
(x3 + 1/sqrt2)^2 + ( 1/sqrt2)^2 + (y3 - 1/sqrt2)^2 + ( 1/sqrt2)^2 = (x3 + y3)^2
x3 * sqrt2 + 1/2 + 1/2 - y3 * sqrt2 + 1/2 + 1/2 = 2 * x3*y3
Finally:
x3 * sqrt2 + 1/2 + 1/2 - y3 * sqrt2 + 1/2 + 1/2 = - 7 * sqrt2 * x3 + 49/2 + 49/2 + 7 * sqrt2 * y3 + 49/2 + 49/2
4 * sqrt2 * x3 + 1 = 4 * sqrt2 * y3 + 49
x3 = y3 + 6 * (2^0.5)
y3 + 6 * (2^0.5) + 2^0.5 - y3 = 2^0.5 * (y3 + 6 * (2^0.5)) *y3

y3 = 5 - 3 * (2^0.5)
x3 = 5 + 3 * (2^0.5)
 
Last edited:
jfl @ solving math problems on an incel forum
you niggas.. inceldom is a hell of a drug..
 
Last edited:
@grondilu
@mNFwTJ3wz9

Yes, good job, the both of you. It turns out that the radius is exactly 5.

Here is my solution
58A9B63B 6AB4 43D7 82F9 67307E8DCD0F

Edit: not AP, i meant the centre of the circle to P. Anyways, I hope my solution is clear
 
Last edited:
WorldYamataizer said:
@grondilu
@mNFwTJ3wz9

Yes, good job, the both of you. It turns out that the radius is exactly 5.

Here is my solution
View attachment 392347
Edit: not AP, i meant the centre of the circle to P. Anyways, I hope my solution is clear
Click to expand...
Nicely done, probably the simplest way to solve it.
 
high iqcels only
 
High IQ thread but didn’t read
 
maths me
 
Prob 0011 : I wanted to see how Mathematica could "solve" it :

Code: 
$ wolframscript
Wolfram Language 12.1.1 Engine for Linux x86 (64-bit)
Copyright 1988-2020 Wolfram Research, Inc.

In[1]:= EuclideanDistance[#[a], #[i]] &@Association[                                                    
          RandomInstance[GeometricScene[                                                                
             {a, b, c, d, e, i},                                                                        
             {                                                                                          
              EuclideanDistance[c, e] == 7,                                                             
              EuclideanDistance[e, d] == 1,                                                             
              PlanarAngle[e -> {b, d}] == \[Pi]/4,                                                      
              EuclideanDistance[a, i] == EuclideanDistance[i, b] ==                                     
               EuclideanDistance[i, c] == EuclideanDistance[i, d],                                      
              GeometricAssertion[{a, i, b}, "Collinear"],                                               
              GeometricAssertion[{Line[{a, b}], Line[{c, d}]}, {"Concurrent", e}]                                                                                     
              }                                                                                         
             ]                                                                                          
            ]["Points"]                                                                                 
          ]                                                                                             

Out[1]= 5.
 
Problem #0012
Hello, .co Math Club.
Due to increased responsibilities from my classes, I’ll take a few days off from posting interesting math problems, before resuming.

If you have any suggestions on specific types of problems you would like to make/share then let me know (e.g. more calculus, geometry, algebra etc.)

58782A5A 2191 49CB 889D C8032CEAF4C8

Triangle ABC is isosceles with AB=AC and BC=65. P is a point on BC such that the perpendicular distances from P to AB and AC are 24 and 36, respectively. Determine the area of triangle ABC, correct to one decimal.
@Divergent_Integral
@SelfCrucified
@grondilu
@mNFwTJ3wz9
@Diocel
@mental_out
@Irredeemable
@Caesercel
@nihility
@Liszt
 
Prob 0012.

Capture dcran de 2021 01 06 23 00 42

I know, it's cheating, but at the same time I get to learn to use Mathematica.

Notice that Mathematica informs me that there is an other solution, with a different area, if we don't impose the points P, R, and S to be on the triangle (which I believe means at least one angle is obtuse).
 
Last edited:
WorldYamataizer said:
Problem #0012
Hello, .co Math Club.
Due to increased responsibilities from my classes, I’ll take a few days off from posting interesting math problems, before resuming.

If you have any suggestions on specific types of problems you would like to make/share then let me know (e.g. more calculus, geometry, algebra etc.)

View attachment 392734
Triangle ABC is isosceles with AB=AC and BC=65. P is a point on BC such that the perpendicular distances from P to AB and AC are 24 and 36, respectively. Determine the area of triangle ABC, correct to one decimal.
@Divergent_Integral
@SelfCrucified
@grondilu
@mNFwTJ3wz9
@Diocel
@mental_out
@Irredeemable
@Caesercel
@nihility
@Liszt
Click to expand...
So lets try to not brute force this one
by similar triangles : RP/SP = BP/BC
also area(ABC) = area(ACP) + area(ABP)
= 0.5 * (AC*SP + AB* RP)
lets say AC = AB = x
(x - 10)^2 + 24^2 = (x - 15)^2 + 36^2
x = 169/2
area = x * (24 + 36) * 1/2
area = 2535
 
Last edited:
mNFwTJ3wz9 said:
So lets try to not brute force this one
by similar triangles : RP/SP = BP/BC
also area(ABC) = area(ACP) + area(ABP)
= 0.5 * (AC*SP + AB* RP)
lets say AC = AB = x
(x - 10)^2 + 24^2 = (x - 15)^2 + 36^2
x = 169/2
area = x * (24 + 36) * 1/2
area = 2535
Click to expand...
Slick. I like it!

The key to this problem was realizing the similar triangles given to you. Here's the way I did it.

Since ABC is isosceles, then angle ACB= angle ABC.
Therefore, triangles BRP and CSP are similar. (Angle, angle)
Suppose BP=x, then PC=65-x
By similarity, 24/36 = x/(65-x). Solving this equation gives x=26. So BP=26 and PC=39.
By the Pythagorean Theorem, BR=10 and CS=15

Dropping a perpendicular A onto BC, call the foot of the altitude M.
Then triangle AMC is similar to triangles BRP and CSP. (shared angle, right angle)
By similarity, AM/36 = (65/2)/15
AM=78.

The area ABC is (1/2)(65)(78)=2535
 
Problem #0013

Hello .co Math Club. Today, we will try to find side lengths of a triangle that satisfy a certain condition. Enjoy.

Three side lengths of a triangle are consecutive integers. The largest angle of the triangle is two times the smallest angle. What are the side lengths of the triangle?

It may be helpful to draw a useful diagram.

@Divergent_Integral
@SelfCrucified
@grondilu
@mNFwTJ3wz9
@Diocel
@mental_out
@Irredeemable
@Caesercel
@nihility
@Liszt
 
WorldYamataizer said:
Problem #0013

Hello .co Math Club. Today, we will try to find side lengths of a triangle that satisfy a certain condition. Enjoy.

Three side lengths of a triangle are consecutive integers. The largest angle of the triangle is two times the smallest angle. What are the side lengths of the triangle?

It may be helpful to draw a useful diagram.

@Divergent_Integral
@SelfCrucified
@grondilu
@mNFwTJ3wz9
@Diocel
@mental_out
@Irredeemable
@Caesercel
@nihility
@Liszt
Click to expand...

As the triangle gets larger, it looks more and more like an equilateral triangle, and such triangle is obviously not the solution, so one can safely assume the solution is small. So we can try with small integer values, and I think {2,3,4} fits. I used the cosine rule to calculate the angles :

a² = b² + c² - 2bc cos(alpha)

The cosines of the two relevant angles are -7/8 and 1/4 (straightforward application of the above formula). Let's name the smallest one x and the largest one y.

cos(2x)=cos(x)² - sin(x)² = cos(x)² - (1 - cos(x)²) = 2 cos(x)² - 1

So :
cos(2x) = 2 (1/4)² - 1 = 2/16 - 1 = 1/8 - 1 = - 7/8,

So 2x has the same cosine as y. Since we're in a triangle the angles are positive and inferior to pi, on which domain the cosine function is injective, thus y = 2x, and therefore the triangle with side lengths 2,3,4 does fit the requirement.
 
Last edited:
WorldYamataizer said:
Problem #0013

Hello .co Math Club. Today, we will try to find side lengths of a triangle that satisfy a certain condition. Enjoy.

Three side lengths of a triangle are consecutive integers. The largest angle of the triangle is two times the smallest angle. What are the side lengths of the triangle?

It may be helpful to draw a useful diagram.

@Divergent_Integral
@SelfCrucified
@grondilu
@mNFwTJ3wz9
@Diocel
@mental_out
@Irredeemable
@Caesercel
@nihility
@Liszt
Click to expand...
triangle abc
angles ABC opposite to corresponding sides
a = x,b = x+1,c = x+2 WLOG
C = 2*A

using the area sin rule -
1/2 * a * b * sin(C) = 1/2 * b * c * sin(A)
a * sin(C) = c * sin(A)
x * sin(2*A) = (x + 2) * sin(A)
x * 2 * sin(A) * cos(A) = (x+2) * sin(A)
cos(A) = (x+2)/ (2*x)

Now another formula -
area = sqrt(s*(s-a)*(s-b)*(s-c))
1/2 * b * c * sin(A) = sqrt( 1.5 * (x+1) *( 0.5*(x + 3) )*( 0.5*(x + 1) )*( 0.5*(x-1) ) )
sin(A) * 0.5 * (x+1) * (x+2) = 0.5 * (x+1) * sqrt( 1.5 *(x + 3) * 0.5 * (x - 1) )
sin(A) = sqrt( 0.75 * (x - 1) * (x + 3) ) / (x + 2)

Finally
sin(A)^2 + cos(A)^2 = 1
((x+2)/(2*x))^2 + 0.75 * (x - 1) * (x + 3) / ((x + 2)^2) = 1
Oh man this is kinda bad, but lets do it...
(x+2)^4 + 0.75 * (x - 1) * ( x + 3 ) * (2x)^2 = (x+2)^2 * (2x)^2
(x^2 + 4x + 4) * (x+2)^2 + 3 * (x^2 + 2x - 3) * x^2 = 4 * x^2 * (x+2)^2
(4x + 4) * (x+2)^2 + 3 * (x^2 + 4x + 4 - 2x - 7) * x^2 = 3 * x^2 * (x+2)^2
(4x + 4) * (x+2)^2 + (- 2x - 7) * x^2 = 0
-2*x^3 - x^2 + 32*x + 16 = 0
2 x^3 + x^2 - 32 x - 16 = 0
Ok I'm not doing a cubic by hand.
x = 4 or -4 or -1/2.
Going with 4
triangle is 4,5,6
grondilu said:
2,3,4
Click to expand...
You sure?
 
Last edited:
mNFwTJ3wz9 said:
You sure?
Click to expand...

I mean, yeah. I'm pretty sure, unless I missed something about the problem statement.

Code: 
    cosineRule[a_, b_, c_] := (a^2 - b^2 - c^2)/(2 b c)
    ArcCos /@ Simplify@Table[cosineRule @@ RotateLeft[{n, n + 1, n + 2}, i], {i, 0, 2}]
    % /. n -> 2
    {Max[%],Min[%]}

does return {ArcCos[-7/8], ArcCos[1/4]}

Mathematica then fails to see that the ratio between those two values is exactly 2, but the numerical value suggests it strongly, and there is the demonstration I gave about it which I think is fairly simple.
 
meanwhile chads measuring foids ass size with their pp
 
grondilu said:
I mean, yeah. I'm pretty sure, unless I missed something about the problem statement.

Code: 
    cosineRule[a_, b_, c_] := (a^2 - b^2 - c^2)/(2 b c)
    ArcCos /@ Simplify@Table[cosineRule @@ RotateLeft[{n, n + 1, n + 2}, i], {i, 0, 2}]
    % /. n -> 2
    {Max[%],Min[%]}

does return {ArcCos[-7/8], ArcCos[1/4]}

Mathematica then fails to see that the ratio between those two values is exactly 2, but the numerical value suggests it strongly, and there is the demonstration I gave about it which I think is fairly simple.
Click to expand...
1610476159633

grondilu said:
cosineRule[a_, b_, c_] := (a^2 - b^2 - c^2)/(2 b c)
Click to expand...
I think you missed a negative sign.
 
Last edited:
You must log in or register to reply here.

Similar threads

JustanotherKanga
Discussion Why Has the West not Collapsed Yet?
Replies
18
Views
289
Grodd
Grodd
ResidentHell
The Only Standard of Objective Morality that Makes Sense is one that isn't concerned with Choice, Intent and Accountability
Replies
1
Views
52
ResidentHell
ResidentHell
IncelGolem
Discussion ISRAEL-HATER MASTER-THREAD: Bring me all of your Israel or Jew lies to destroy
Replies
28
Views
574
AtrociousCitizen
AtrociousCitizen
Regenerator
Serious Signs a user has a low IQ
Replies
31
Views
574
Emba
Emba
JustanotherKanga
Serious Who Am I, And What Do I Stand For?
Replies
20
Views
140
go2sleep
go2sleep

Users who are viewing this thread

Total: 6 (Incels: 0, Bluepillers: 6)

Follow Us On Social Media

615,052Threads
14,057,480Posts
27,724Members
DoomedvirginNew Lost Soul

About Us

Incels.is is a community for men that struggle with or are unable to get into romantic relationships with women despite trying. We welcome men from all walks of life, and from all cultural and racial backgrounds, as long as you are an incel.

Online statistics

Members online
216
Guests online
2,032
Total visitors
2,248
Totals may include hidden visitors.
shape1
shape2
shape3
shape4
shape5
shape6
Back
Top